find the contest here
Ammalgam is both an AMM and a lending protocol. The idea is they use the same liquidity for both, which allows for higher yield for LPs. In order to not break everything, they have to keep track of a usage rate. Whenever the rate is too high, swaps are charged are significantly higher fee.
Imagine a pool with 100 ETH and 200k USDC, and in a single block most of the ETH was sold for USDC. To prevent market manipulation (MEV, flash swaps, gigadumping shitcoins, etc) they set the reserves at the start of the block as reference, and charge a fee based on how far from them your swap will leave the pool. They use 3 calculations to charge the fee depending on the state of the reserves.
If your swap brings the current reserves back to reference, you are charged the lowest fee allowed, 0.1 BIPS. If you're swapping away from the reserves, you are charged a complex quadratic equation up to 4000 BIPS. Past this point you reach the final level, where the fee growth becomes linear and you're charged > 4000.
See if you can spot the issue yourself.
This graph shows the base case: First swap in a pool, selling ETH for USDC. The X axis is the size of the input, and the Y axis the fee in BIPS. The red line highlights the point where the code switches from quadratic to linear. The function HAS to be continuous, which means both the quadratic and linear fee calculation have to return 4000 BIPS at the transition point.

However, this is what it looks like when the reserves are off reference, for the 2nd swap in a block onwards:
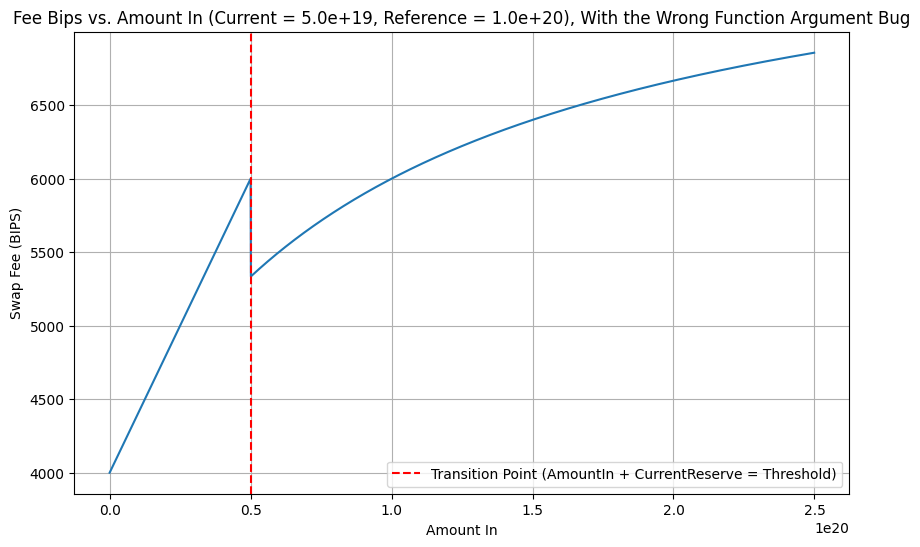
To find this, I took the fee calculation below and converted to python. Then by changing some parameters and plotting, I was able to visualize that the transition point is not achieved at 4000 BIPS, but much later instead. All the plots you're in this post were made in that notebook.
But when I was writing the PoC for the bug, when comparing the fee charged in a swap vs the pure function, the numbers were completely off. This is when I found out the first issue:
uint256 fee = QuadraticSwapFees.calculateSwapFeeBipsQ64(amountIn, reserve, referenceReserve);
function calculateSwapFeeBipsQ64(
uint256 input,
uint256 referenceReserve,
uint256 currentReserve
) internal pure returns (uint256 fee) {
The order of the parameters are wrong, this is why the graphics were so off (I thought) and why my PoCs were giving me nightmares. This was the 1st submitted bug, very simple, had 11 duplicates, took 10 minutes to write that report. An AI could easily have found this.
Knowing this bug, we go back to the notebook and pass the *correct* parameters instead. We now see the issue remains, but get a glimpse of what the real bug looks like:
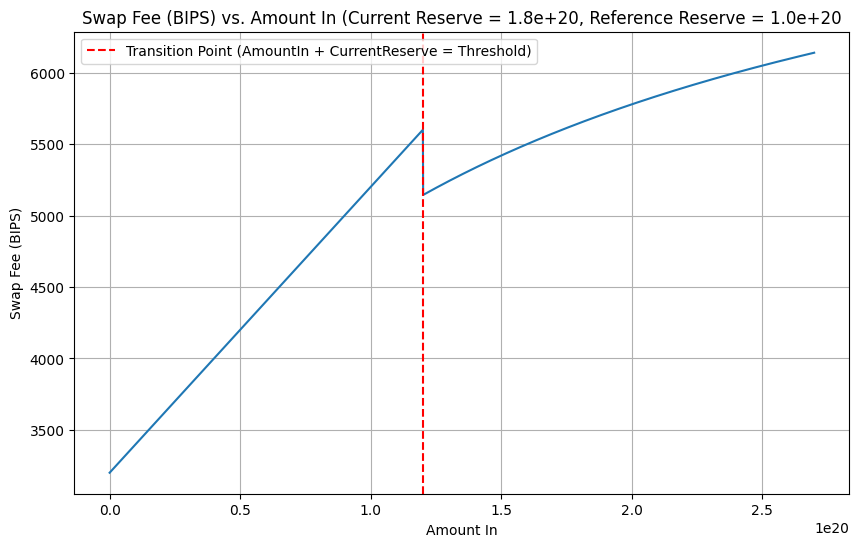
For the 2nd swap onwards, the fee function is NOT continuous. This breaks a key invariant, if users knew this they could purposefully trade away from the reserves in order to be charged less rather than more.
Looking at the code we find out why that happens. The line below is an if block inside the calculateSwapFeeBipsQ64 function that determines whether the swap has left the quadratic range.
...
} else if (input + currentReserve > referenceReserve * LINEAR_START_REFERENCE_SCALER) {
// This swap passes beyond the max quadratic fee
fee = MAX_QUADRATIC_FEE_PERCENT_BIPS * (
TWO_Q64 - Convert.mulDiv(
referenceReserve,
MAX_QUADRATIC_FEE_Q64,
N * (input + 2 * (currentReserve - referenceReserve)),
false
)
);
...This works for the 1st swap because \(currentReserve = referenceReserve\). But for the case where \(currentReserve > referenceReserve\), this `if` block is checking whether we surpassed the threshold using the `input` and the current state of the reserve.
To find out mathematically when the code should enter this block, we need to find the `input` to the linear formula that returns 4000 BIPS. This happens when the fee equals `MAX_QUADRATIC_FEE_PERCENT_BIPS`. To reach this value, the `mulDiv` block must be equal to one, which means the dividend and divisor must be equal.
This gives us the equation:
$$1 = \frac{referenceReserve \times MAX\_QUADRATIC\_FEE\_Q64}{N \times (input + 2 \times (currentReserve - referenceReserve))}$$
Since \(MAX\_QUADRATIC\_FEE\_Q64\) is 40 in Q64, we can simplify the constants:
$$1 = \frac{referenceReserve \times 40}{20 \times (input + 2 \times (currentReserve - referenceReserve))}$$
Solving for the denominator gives us:
$$input + 2 \times (currentReserve - referenceReserve) = referenceReserve \times 2$$
In terms of `LINEAR_START_REFERENCE_SCALER` (which equals 3), we get:
$$input + (currentReserve - referenceReserve) + referenceReserve$$
$$ = LINEAR_START_REFERENCE_SCALER \times referenceReserve$$
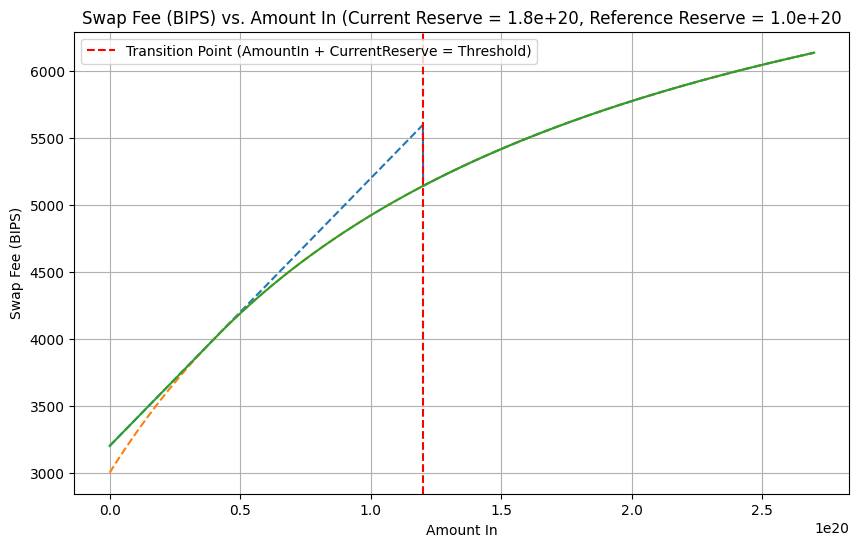
Which is different from the condition in the code. The current code is missing the second term, which causes it to enter the linear equation too late creating the discontinuity. The fix is to use the correct if comparison. Below I show a graph comparing the original formula and the fixed one, notice that the function becomes much smoother.
Since I had a pretty good notebook setup already, I decided to run an invariant check. Was it possible for the fee to be lower than the minimum allowed? To do this, we start with a current reserve lower than reference and check if the graph at any point has reached a BIPS lower than 0.1. As it turns out, the invariant was broken.
if (input + currentReserve > referenceReserve) {
// the input moves from the current reserve past the starting reserve, we charge a
// weighted fee based on how far past the starting reserve we are
uint256 pastBy = input + currentReserve - referenceReserve;
if (input + currentReserve > referenceReserve * LINEAR_START_REFERENCE_SCALER) {
...
} else {
// this fee is still in the quadratic range
fee = Convert.mulDiv(N_TIMES_BIPS_Q64_PER_PERCENT, pastBy, referenceReserve, false);
}
fee = Convert.mulDiv(fee, pastBy, input, false);
This is the portion of the code that goes from minimum to quadratic. The problem here is that if the reference is too close to current reserve, pastBy will be ~ input. If the input brings the reserves back to balance, the fee rounds to zero.
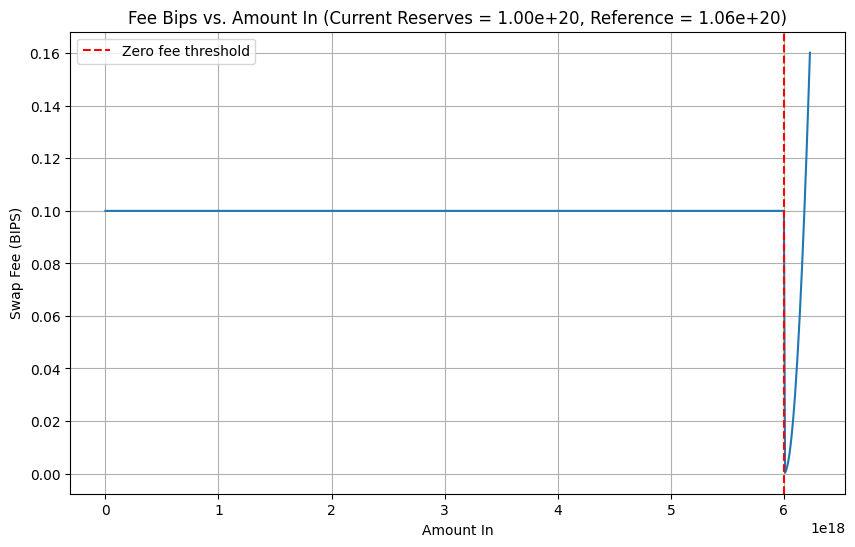
This can be fixed by adding a minimum fee check after the fee calculation, if fee < 0.1 BIPS, fee = 0.1 BIPS.
The incorrect quadratic formula bug was a solo medium, and the extra bug had a single duplicate. The alpha here is that a lot of SRs are either skipping or not fully understanding complex mathematical equations, leaving plenty of opportunities on the table. But if you read this article carefully, you'll notice that I didn't actually had to run the numbers inside the equation to find the bug, but rather, converted the function to python and analyzed it with my parameters of choice.
To find the issue without plotting, you'd have to realize by yourself that 1) there's an invariant that the fee transition must be continuous at all points and 2) verify this invariant for reserves off reference. Creating this notebook ended up as a shortcut to both. This is a practice I've included to my auditing method when dealing with heavy mathematics, or functions with excessive amounts of branch pathing. Many veteran auditors deal with these situations in their own way, phil uses a spreadsheet, 0x52 keeps in his head somehow. Regardless, you need to have a plan of action for these occasions, unless you wanna miss them on purpose.
return